Problém 100 väzňov

Problém 100 väzňov je matematický problém z teórie pravdepodobnosti a kombinatoriky. Aby väzni prežili, musia všetci nájsť svoje vlastné číslo v jednom zo 100 zásuviek, pričom každý väzeň môže otvoriť iba 50 zásuviek a nemôže s ostatnými väzňami komunikovať. Na prvý pohľad vyzerá situácia beznádejná, ale existuje stratégia, ktorá dáva väzňom realistickú šancu na prežitie. Problém bol prvýkrát sformulovaný v roku 2003 dánskym informatikom Peter Bro Miltersenom.

V probléme 100 väzňov každý väzeň musí nájsť svoje číslo v jednom zo 100 zásuviek, ale môže ich otvoriť iba 50.

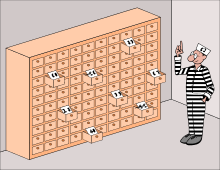
Zadanie

Problém 100 väzňov bol rôzne formulovaný v rôznymi autormi. Následujúca verzia je volným prekladom zadania podľa Phillippe Flajoleta a Roberta Sedgewicka:

Riaditeľ väznice sa rozhodne dať poslednú šancu svojim 100 väzňom odsúdeným na smrť. Do svojej kancelárie, kde má 100 zásuviek (označených číslami 1-100) náhodne umiestni kartičky s číslami väzňov, ktorí sú tiež označení číslami 1-100. Väzni majú po jednom vchádzať do kancelárie. Každému dovolí otvoriť najviac 50 zásuviek. Z miestnosti odchádzajú inou chodbou, nemajú ako podať ďalším čakajúcim väzňom informácie. Riaditeľ väznice sa rozhodol, že omilostí všetkých väzňov, ale iba (práve) vtedy, keď sa každému z väzňov podarí nájsť svoje číslo v jednej z 50 otvorených zásuviek. Ak čo len jeden z nich svoje číslo nenájde, všetci zomrú. Akú stratégiu majú väzni použiť, ak chcú mať čo najväčšiu šancu prežiť?

Riešenie

Ak každý väzeň otvorí 50 zásuviek náhodne, pravdepodobnosť, že jednotlivý väzeň nájde svoje číslo je 50%. Teda súhrnná pravdepodobnosť pre všetkých je súčin pravdepodobností jednotlivcov:

$\underbrace {\left({\frac {1}{2}}\right)\cdot \left({\frac {1}{2}}\right)\cdot \ldots \cdot \left({\frac {1}{2}}\right)} _{100\times }=\left({\frac {1}{2}}\right)^{100}\approx 0.0000000000000000000000000000008$

To je veľmi, veľmi malé číslo. Situácia vyzerá pre väzňov beznádejne.

Stratégia

Prekvapivo, existuje stratégia, ktorá dáva väzňom šancu prežiť s viac než 30% pravdepodobnosťou. Dôležité uvedomiť si je, že väzňom nezáleží na tom, aby čo najviac z nich našlo svoje číslo, ale na tom, aby všetci našli svoje číslo.

Víťazná stratégia je následovná:

1. Každý väzeň otvorí zásuvku, ktorá má jeho číslo.
2. Ak táto zásuvka obsahuje jeho číslo, ukončí hľadanie a bol úspešný.
3. V opačnom prípade zásuvka obsahuje číslo iného väzňa. Väzeň otvorí zásuvku s číslom toho iného väzňa.
4. Väzeň opakuje kroky 2 a 3 až kým nenájde svoje číslo alebo otvorí 50 zásuviek.

Tento prístup zaručuje, že nebude otvárať zásuvky opakovane. Môžeme si všimnúť, že ak sa mu niekedy podarí „uzavrieť cyklus“ - teda dostať sa naspäť do prvej otvorenej zásuvky, tak posledná otvorená zásuvka obsahuje jeho číslo (odkázala ho na zásuvku s jeho číslom, teda musela obsahovať jeho číslo).

Príklady

Ukážeme si, že táto stratégia znie pre väzňov relatívne výhodne. Uvážime zmenšenú situáciu s 8 väzňami a 8 zásuvkami, kde každý väzeň smie otvoriť 4 zásuvky. Riaditeľ rozmiestnil čísla do zásuviek následovne:

číslo zásuvky	1	2	3	4	5	6	7	8
číslo väzňa	7	4	6	8	1	3	5	2

Väzni konajú následovne:

• Väzeň 1 otvorí zásuvku 1 a nájde čislo 7. Otvorí zásuvku 7 a nájde číslo 5. Otvorí zásuvku 5 a nájde číslo 1, teda jeho číslo, čiže uspel.
• Väzeň 2 otvorí zásuvky 2, 4 a 8 v tomto poradí. V poslednom nájde svoje číslo.
• Väzeň 3 otvorí zásuvky 3 a 6, kde nájde svoje číslo.
• Väzeň 4 otvorí zásuvky 4, 8 a 2, kde nájde svoje číslo. Všímavý čitateľ si mohol toto odvodiť z konanie väzňa 2.
• Podobne aj väzni 5 až 8 nájdu svoje čísla (dá sa odvodiť z predchádzajúcich informácií).

V tomto prípade všetci väzni boli úspešní. To sa však nestane vždy (na veľké sklamanie väzňov). Uvažme následovné rozostavenie čísel riaditeľom:

číslo zásuvky	1	2	3	4	5	6	7	8
číslo väzňa	3	1	7	5	8	6	4	2

V tomto prípade väzeň 1 otvorí zásuvky 1, 3, 7 a 4, otvorením ktorej musí skončiť, lebo nenašiel svoje číslo a viac ako 4 zásuvky otvoriť nemôže. Bol neúspešný, teda ďalší väzni už nemusia ani hrať, všetci budú popravení.

Reprezentácia permutáciami

Reprezentácia permutácie (1 7 5)(2 4 8)(3 6) grafom.

Reprezentácia permutácie (1 3 7 4 5 8 2)(6) grafom.

Riaditeľovo rozloženie čísel do zásuviek sa dá matematicky popísať permutáciami čísel 1 až 100. Permutácie sú bijektívne zobrazenia (funkcie) z množiny prirodzených čísel $\mathbb {N}$. V našom prípade je to teda bijektívna funkcia: $p:\{1,2,\ldots ,100\}\to \{1,2,\ldots ,100\}$

Intuitivne si funkciu permutácie predstavíme ako „iné usporiadanie“ prvkov definičného oboru.

Každá permutácia sa dá rozložíť na tzv. cykly permutácie (postupnosť čísel, ktoré keď zobrazujem permutačnou funkciu sa eventuálne „vráti“ do prvej hodnoty). Uvedomíme si, že tieto cykly sú vždy disjunktné -- nepretínajú sa, nemajú spoločné hodnoty. Permutáciu z prvého príkladu rozpíšeme v tzv. cyklovom zápise následovne:

$(1\,\,7\,\,5)(2\,\,4\,\,8)(3\,\,6)$

Pozostáva teda z dvoch cyklov dĺžky 3 a jedného cyklu dĺžky 2. Permutáciu z príkladu 2 zapíšeme následovne:

$(1\,\,3\,\,7\,\,4\,\,5\,\,8\,\,2)(6)$

Pozostáva z jedného cyklu dĺžky 7 a jedného cyklu dĺžky 1.

Uvedomíme si, že ak sa v cyklovom zápise rozostavení čísel do zásuviek nachádza cyklus dĺžky väčšej ako počet dovolených otvorení zásuviek, väzni (používajúc túto stratégiu) musia nutne prehrať -- ak by permutácia v horeuvedených príkladoch mala cyklus dĺžky 5 a viac, všetci väzni, ktorých čísla sú v tomto cykle by prehrali po štyroch otvoreniach.

Pravdepodobnosť úspechu stratégie

Pravdepodobnosťná distribúcia dĺžky najdlhšieho cyklu v náhodnej permutácií čísel 1 až 100. Zelená plocha odpovedá pravdepodobnosti prežitia väzňov.

Vieme, že aj napriek stratégií môžu väzni prehrať. Majú však lepšiu šancu na výhru ako bez nej? Táto otázka sa dá zjednodušiť na otázku: „Zo všetkých permutácií na množine $\{1,2,\ldots ,100\}$, koľko obsahuje cyklus s dĺžkou väčšou ako 50?“ Na túto otázku dokážeme už číselne odpovedať!

Uvedomíme si, že permutácia čísel 1 až 100 môže obsahovať najviac jeden cyklus s dĺžkou $l>50$. Existuje presne ${\binom {100}{l}}$ spôsobov, ako vybrať čísla, ktoré budú do tohoto cyklu patriť (viete z kombinatoriky). V rámci cyklu môžeme čísla usporiadať $(l-1)!$ spôsobmi -- čísla usporiadame $l!$ spôsobmi, ale každé usporiadanie sa tam bude opakovať $l$-krát, iba bude otočené -- teda stále ten istý cyklus -- platí: ${\frac {l!}{l}}=(l-1)!$. Zvyšné čísla, nepatriace cyklu, usporiadame $(100-l)!$ spôsobmi. Celkový počet vhodných permutácií je teda:

${\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}$

Pravdepodobnosť, že náhodná permutácia obsahuje cyklus dĺžky väčšej ako 50 spočítame následovne (pomocou pravidla o nezávislých javoch):

${\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=H_{100}-H_{50}$

kde $H_{n}$ je $n$-té harmonické číslo $\left(H_{n}=\sum _{i=1}^{n}{\frac {1}{n}}={\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+\ldots +{\frac {1}{n}}\right)$.

Pravdepodobnosť, že náhodná permutácia neobsahuje žiadny cyklus dĺžky väčšej ako 50 spočítame následovne (pomocou pravidla o opačnom jave):

$1-(H_{100}-H_{50})\approx 0.31183$

Väzni prežijú pomocou stratégie permutačných cyklov s pravdepodobnosťou väčšou než 30%!

Asymptotika

Harmonické čísla sú odhadom daným plochou pod hyperbolou -- dajú sa teda odhadnúť logaritmom.

Ak uvážime $2n$ väzňov namiesto 100, kde $n\in \mathbb {N}$ je ľubovolné prirodzené číslo, pravdepodobnosť prežitia väzňov s cyklovou stratégiou je daná:

$1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2$

S Euler-Mascheroniovou konštantou $\gamma$ pre $n\to \infty$

$\lim _{n\to \infty }(H_{n}-\ln n)=\gamma$

platí, čo vedie k asymptotickej pravdepodbnosti prežitia:

$\lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685$

Postupnosť pravdepodobností je nerastúca (monotónna), pravdepodobnosť prežitia väzňov je väčšia ako 30%, nezávisle od počtu väzňov.

Optimalita

V 2006, Eugene Curtin a Max Warshauer (z University of Texas) dodali dôkaz optimality tejto cyklovej stratégie. Dôkaz je založený na ekvivalencí s podobným problémom, kde väzni majú dovolené byť prítomní v miestnosti a pozorovať otváranie zásuviek inými väzňami. Táto ekvivalencia je založená na ekvivalencí cyklického zápisu a jednoriadkového zápisu permutácií (spodný riadok dvojriadkového zápisu). V tomto probléme je nezávisle na stratégií pravdepodobnosť prežitia rovná pravdepodobnosti v pôvodnom probléme. Keďže ľubovolná stratégia z pôvodného problému sa dá aplikovať na pozmenený problém, ale nikdy nedosiahne väčšiu úspešnosť, musí byť cyklová stratégia optimálna.

Pozri aj

• Väzňova dilema
• Problém troch väzňov

Literatúra

• Philippe Flajolet, Robert Sedgewick. Analytic Combinatorics. [s.l.] : Cambridge University Press, 2009. ISBN 978-1-139-47716-1.
• Richard P. Stanley. Algebraic Combinatorics: Walks, Trees, Tableaux, and More. [s.l.] : Springer, 2013. (Undergraduate Texts in Mathematics.) ISBN 978-1-461-46998-8.
• Peter Winkler. Mathematical Mind-Benders. [s.l.] : Taylor and Francis, 2007. ISBN 978-1-568-81336-3.

Externé odkazy

• Rob Heaton: Mathematicians hate civil liberties - 100 prisoners and 100 boxes, 13. januára 2014 (po anglicky)
• Oliver Nash: Pity the prisoners, 12. decembra 2009 (po anglicky)
• Jamie Mulholland: Prisoners in Boxes, jar 2011 (PDF) (po anglicky)
• MinutePhysics: An Impossible Bet a Solution to The Impossible Bet, 8. decembra 2014 (po anglicky)